Integrating Diverse Approaches to the Reliability of Engineering Structures: Refinement of the Fracture Model for Pressure Piping
TWI Industrial Member Report 1167-2023 [pdf / 753 KB]
By Isabel Hadley, Charles Schneider & Yin Jin Janin
Industrial Need
The probability of failure, POF (the converse of which is ‘reliability’) of engineering components and structures depends on numerous factors, including design, manufacture, inspection, operation and human factors. Reliability may be calculated on the basis of direct observation (what proportion of components fail prematurely?) or theoretical methods (what failure mechanisms are possible, and how likely is it that the conditions for failure will be present during operation?), or some mixture of the two. In this study, two methods are used to estimate probability of failure, using approaches drawn from a range of standards, and comparing the outcomes with situations related to other standards. Relevant documents include BS 7910 (BSI, 2019), R6 (EDF Energy, 2001), API 581 (API, 2016), PD 5500 (BSI, 2018) and EN 13445 (BSI, 2014), and ASME B31.3 (ASME, 2018):
- A ‘top-down’ method based on a mixture of failure statistics and engineering judgement.
- A ‘bottom-up’ method based on fracture mechanics/engineering critical assessment (ECA). Both ‘deterministic’ (using a single characteristic value of each variable) and probabilistic approaches were used, the latter allowing direct estimation of probability of failure.
Key Findings
- The values of probability of failure (POF) determined using the RBI approach are somewhat lower than those presented previously in Stage 1, because of the changed assumptions regarding the relationship between Charpy test temperature and service temperature.
- The relative benefit of applying post-weld heat treatment (PWHT) vs joints in as-welded (AW) condition, ie POFAW/POFPWHT, is 8.3, ie around one order of magnitude, similar to the magnitude reported previously.
- When assessing using probabilistic fracture mechanics (PFM), as more probabilistic variables are added, so the POF falls, reflecting increasingly realistic treatment of variables such as WRS and flaw size compared with the preliminary results presented in the earlier report.
- The flaw size distribution after inspection is an approximation, and will tend to overestimate the actual POF.
- The residual stress distribution has a high value of standard deviation (SD).
- When flaw height, a, is treated as a probabilistic variable without linking it to the flaw length, 2c, flaw shapes are produced that are outside the validity limits of BS 7910 analytical solutions.
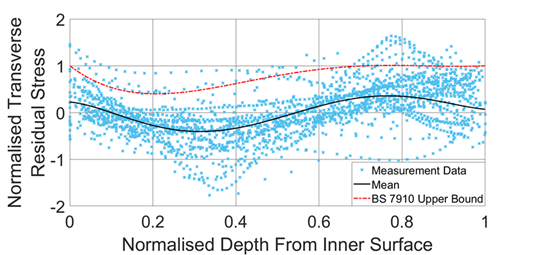
Girth weld database results for ‘low’ heat input welds, showing best fit to data, alongside the current Level 2 upper bound WRS profile. Note: y-axis is normalised to yield strength and x-axis is normalised to thickness.
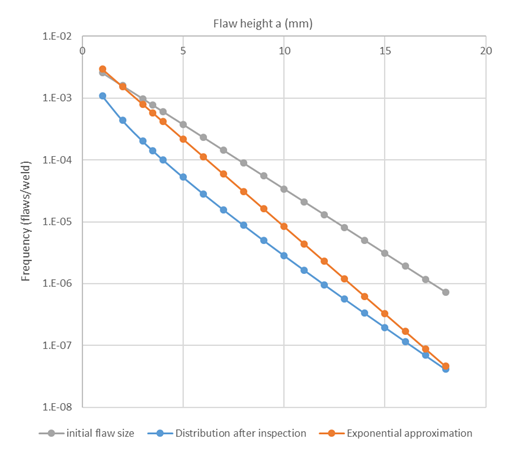
Flaw size distribution for Case 2 (before and after inspection).